Mathematical model describing the decision-making process of a swarm of honeybees for selecting one nest-site among many
N.F. Britton, N.R. Franks, S.C. Pratt, T.D. Seeley, Deciding on a new home: how do honeybees agree ?, Proceedings of the Royal Society of London. Series B: Biological Sciences 269 (1498), 1383-1388 (2002) [Link]
\[ \begin{array}{lcl} X(0) & = & \mathcal{N} (475,5) \\ Y_1(0) & = & \mathcal{U} (350,500) \\ Y_2(0) & = & \mathcal{U} (100,150) \\ Z_1(0) & = & \mathcal{N} (35,1.5) \\ Z_2(0) & = & \mathcal{N} (35,1.5) \\ & & \\ \dot{X} & = & -\beta_1 XY_1 - \beta_2 XY_2 \\ \dot{Y_1} & = & \beta_1 XY_1 -\gamma Y_1 + \delta \beta_1 Y_1 Z_1 + \alpha \beta_1 Y_1 Z_2\\ \dot{Y_2} & = & \beta_2 XY_2 -\gamma Y_2 + \delta \beta_2 Y_2 Z_2 + \alpha \beta_2 Y_2 Z_1\\ \dot{Z_1} & = & \gamma Y_1 - \delta \beta_1 Y_1 Z_1 - \alpha \beta_2 Y_2 Z_1\\ \dot{Z_2} & = & \gamma Y_2 - \delta \beta_2 Y_2 Z_2 - \alpha \beta_1 Y_1 Z_2\\ & & \\ \beta_1,\beta_2 & = & 0.001\\ \gamma & = & 0.3\\ \delta & = & 0.5\\ \alpha & = & 0.7\\ \end{array}\]
Description
The population of the honeybees is divided in three main groups: X are the bees that are neutral (or unbelievers) in the decision, Y is the class of the bees that believes either in one site (Y1) or in another site (Y2) and they are actively spreading their beliefs (called evangelical bees) to the other bees, Z is the class of the bees that believes either in one site (Z1) or in the other site (Z2) but they do not spread (called not-evangelical bees) their beliefs to the others.
Probabilistic Program Computing the Bees Model (Source Code)
x = Normal(475, 5)
y1 = Uniform(350, 400)
y2 = Uniform(100, 150)
z1 = Normal(35, 1.5)
z2 = Normal(35, 1.5)
#dt = 0.1
#beta = 0.001 - We assume that beta = beta1 = beta2
#gamma = 0.3
#delta_beta = 0.0005 - delta * beta
#alpha_beta = 0.0007 - alpha * beta
while true:
x, y1, y2, z1, z2 = x + dt*((-beta)*x*y1 - beta*x*y2), y1 + dt*(beta*x*y1 - gamma*y1 + delta_beta *y1*z1 + alpha_beta*y1*z2), y2 + dt*(beta*x*y2 - gamma*y2 + delta_beta*y2*z2 + alpha_beta*y2*z1), z1 + dt*(gamma*y1 - delta_beta*y1*z1 - alpha_beta*y2*z1), z2 + dt*(gamma*y2 - delta_beta*y2*z2 - alpha_beta*y1*z2)
end
| Program features | Value | Dependency Graph |
|---|---|---|
| if statements | Yes | (L) Linear (NL) nonlinear 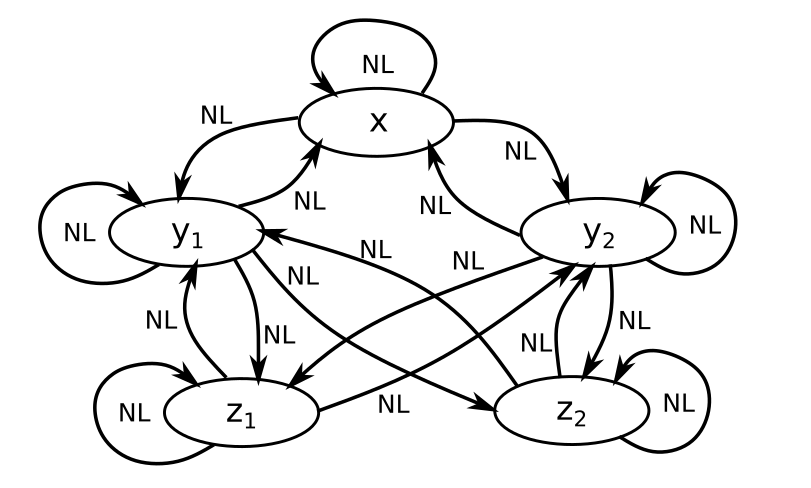 |
| State space | Infinite, continuous | |
| Circular Dependency | Yes | |
| Symbolic Constants | Yes | |
| Effective Variables | No | |
| Defective Variables | Yes (x, y1, y2, z1, z2) |
Probabilistic Program Simulation:
| Parameter | Current Value | Tuning |
|---|---|---|
| Number of program executions: | ||
| Number of loop iterations (n): | ||
| Integration step (dt): | ||
| Parameter (beta): | ||
| Parameter (gamma): | ||
| Parameter (delta): | ||
| Parameter (alpha): |