ProbInG

Parametric Binomial (Source Code):

x = 0
while true:
    x = x + 1 {p} x
end

Program features	Value	Dependency Graph
if statements	No	(L) Linear (NL) nonlinear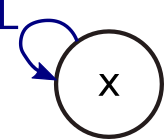
State space	infinite, discrete
Circular Dependency	No
Symbolic Constants	Yes (p)
Effective Variables	Yes (x)
Defective Variables	No

Computing the first moment for the random variable x using POLAR:

python polar.py benchmarks/old/binomial --goals "E(x)"

8888888b.   .d88888b.  888             d8888 8888888b.
888   Y88b d88P" "Y88b 888            d88888 888   Y88b
888    888 888     888 888           d88P888 888    888
888   d88P 888     888 888          d88P 888 888   d88P
8888888P"  888     888 888         d88P  888 8888888P"
888        888     888 888        d88P   888 888 T88b
888        Y88b. .d88P 888       d8888888888 888  T88b
888         "Y88888P"  88888888 d88P     888 888   T88b

By the ProbInG group



-------------------
- Analysis Result -
-------------------

E(x) = 0; n*p
Solution is exact

Elapsed time: 0.3568592071533203 s

Solution for first moment: \[\mathbb{E} (x_n) = n p\]

Computing the second moment for the random variable x using POLAR:

python polar.py benchmarks/old/binomial --goals "E(x^2)"

8888888b.   .d88888b.  888             d8888 8888888b.
888   Y88b d88P" "Y88b 888            d88888 888   Y88b
888    888 888     888 888           d88P888 888    888
888   d88P 888     888 888          d88P 888 888   d88P
8888888P"  888     888 888         d88P  888 8888888P"
888        888     888 888        d88P   888 888 T88b
888        Y88b. .d88P 888       d8888888888 888  T88b
888         "Y88888P"  88888888 d88P     888 888   T88b

By the ProbInG group



-------------------
- Analysis Result -
-------------------

E(x**2) = 0; n*p*(p*(n - 1) + 1)
Solution is exact

Elapsed time: 0.4016072750091553 s

Solution for the second moment: \[\mathbb{E} (x_n^2) = n p (p (n - 1) + 1)\]

Computing the third moment for the random variable x using POLAR:

python polar.py benchmarks/old/binomial --goals "E(x^3)"

8888888b.   .d88888b.  888             d8888 8888888b.
888   Y88b d88P" "Y88b 888            d88888 888   Y88b
888    888 888     888 888           d88P888 888    888
888   d88P 888     888 888          d88P 888 888   d88P
8888888P"  888     888 888         d88P  888 8888888P"
888        888     888 888        d88P   888 888 T88b
888        Y88b. .d88P 888       d8888888888 888  T88b
888         "Y88888P"  88888888 d88P     888 888   T88b

By the ProbInG group



-------------------
- Analysis Result -
-------------------

E(x**3) = 0; n*p*(n**2*p**2 - 3*n*p**2 + 3*n*p + 2*p**2 - 3*p + 1)
Solution is exact

Elapsed time: 0.5916872024536133 s

Solution for the third moment: \[\mathbb{E} (x_n^3) = n p (n^2 p^2 - 3 n p^2 + 3 n p + 2p^2 - 3p + 1)\]

Computing the fourth moment for the random variable x using POLAR:

python polar.py benchmarks/old/binomial --goals "E(x^4)"

8888888b.   .d88888b.  888             d8888 8888888b.
888   Y88b d88P" "Y88b 888            d88888 888   Y88b
888    888 888     888 888           d88P888 888    888
888   d88P 888     888 888          d88P 888 888   d88P
8888888P"  888     888 888         d88P  888 8888888P"
888        888     888 888        d88P   888 888 T88b
888        Y88b. .d88P 888       d8888888888 888  T88b
888         "Y88888P"  88888888 d88P     888 888   T88b

By the ProbInG group



-------------------
- Analysis Result -
-------------------

E(x**4) = 0; n*p*(n**3*p**3 - 6*n**2*p**3 + 6*n**2*p**2 + 11*n*p**3 - 18*n*p**2 + 7*n*p - 6*p**3 + 12*p**2 - 7*p + 1)
Solution is exact

Elapsed time: 0.7818460464477539 s

Solution for the fourth moment: \[\mathbb{E} (x_n^4) = n p (n^3 p^3 - 6 n^2 p^3 + 6 n^2 p^2 + 11 n p^3 - 18 n p^2 + 7 n p - 6 p^3 + 12 p^2 - 7 p + 1)\]

Program simulation:

Parameter	Current Value	Tuning
Number of program executions:
Number of loop iterations (n):
Probability (p):

Exact E(x)	Approx. E(x)	Exact E(x²)	Approx. E(x²)

Exact E(x³)	Approx. E(x³)	Exact E(x⁴)	Approx. E(x⁴)