Coupon Collector Problem - Three Coupons (Source Code)
c0, c1, c2 = 0, 0, 0
new_box = 1
boxes = 0
while new_box == 1:
coupon = Categorical(1/3,1/3,1/3)
if coupon == 0:
c0 = 1
elif coupon == 1:
c1 = 1
else:
c2 = 1
end
boxes = boxes + new_box
new_box = 1 - c0*c1*c2
end
Description
There are boxes of cereals offering inside special coupons of two different types.
One needs to collect at least one coupon of each different type to win an award.
What is the expected number of boxes one needs to open in order
to collect all different coupons at least one time ?
A description of the general Coupon Collector Problem is explained here.
Click here to see the Coupon Collector Problem with two coupons.
Click here to see the Coupon Collector Problem with four coupons.
| Program features | Value | Dependency Graph |
|---|---|---|
| if statements | Yes | (L) Linear (NL) nonlinear 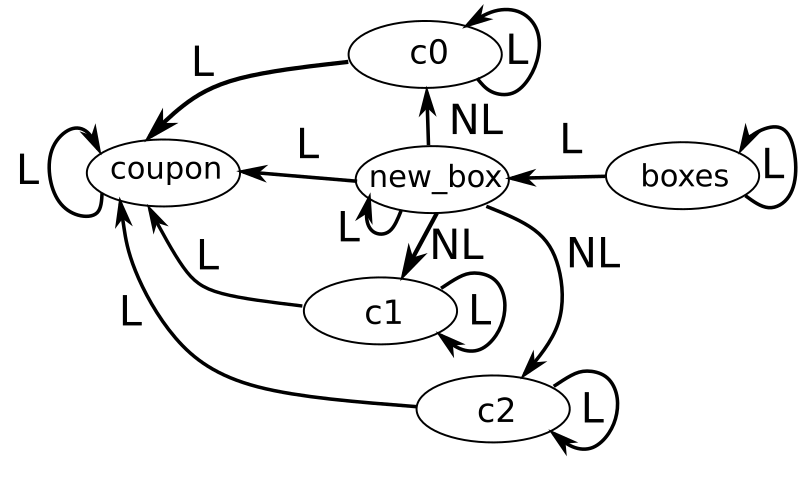 |
| State space | Infinite, discrete | |
| Circular Dependency | Yes | |
| Symbolic Constants | No | |
| Effective Variables | Yes (all) | |
| Defective Variables | No |
Solving the problem using POLAR:
The expected number of boxes can be calculated using POLAR as: \[\mathbb{E} (boxes) = \frac{11}{2} - 9 \left (\frac{2}{3} \right)^n + \frac{9}{2 \cdot 3^n} \]
python polar.py benchmarks/coupon_collector3.prob --goals "E(boxes)"
8888888b. .d88888b. 888 d8888 8888888b.
888 Y88b d88P" "Y88b 888 d88888 888 Y88b
888 888 888 888 888 d88P888 888 888
888 d88P 888 888 888 d88P 888 888 d88P
8888888P" 888 888 888 d88P 888 8888888P"
888 888 888 888 d88P 888 888 T88b
888 Y88b. .d88P 888 d8888888888 888 T88b
888 "Y88888P" 88888888 d88P 888 888 T88b
By the ProbInG group
------------------
- Parsed program -
------------------
_t0 = 0
_t1 = 0
_t2 = 0
c0 = _t0
c1 = _t1
c2 = _t2
new_box = 1
boxes = 0
while new_box == 1:
coupon = Categorical(1/3, 1/3, 1/3)
if coupon == 0:
c0 = 1
else if coupon == 1:
c1 = 1
else:
c2 = 1
boxes = boxes + new_box
new_box = 1 - c0*c1*c2
end
-----------------------
- Transformed program -
-----------------------
types
c0 : Finite(0, 1)
c1 : Finite(0, 1)
c2 : Finite(0, 1)
new_box : Finite(0, 1)
_old3 : Finite(0, 1)
coupon : Finite(0, 1, 2)
end
c0 = 0
c1 = 0
c2 = 0
new_box = 1
boxes = 0
while true:
_old3 = new_box
coupon = Categorical(1/3, 1/3, 1/3) | _old3 == 1 : coupon
c0 = 1 | (coupon == 0 ∧ _old3 == 1) : c0
c1 = 1 | ((¬(coupon == 0) ∧ coupon == 1) ∧ _old3 == 1) : c1
c2 = 1 | ((¬(coupon == 0) ∧ ¬(coupon == 1)) ∧ _old3 == 1) : c2
boxes = boxes + new_box | _old3 == 1 : boxes
new_box = 1 - c0*c1*c2 | _old3 == 1 : new_box
end
-------------------
- Analysis Result -
-------------------
E(boxes) = 0; 1; 2; 3; 34/9; 13/3; 382/81; 403/81; -9*(2/3)**n + 11/2 + 9*3**(-n)/2
Solution is exact
Elapsed time: 0.7428438663482666 s
Comparison with Monte Carlo simulation:
| Parameter | Current Value | Tuning |
|---|---|---|
| Number of program executions: | ||
| Number of loop iterations (n): |
| Exact E(boxes) | Approx. E(boxes) |
|---|---|