Duelling Cowboys (Source Code)
turn = 0
stop = 0
ahit = 0
bhit = 0
while true:
if turn == 0:
ahit = Bernoulli(a)
if ahit == 1:
stop = 1
else:
turn = 1
end
else:
bhit = Bernoulli(b)
if bhit == 1:
stop = 1
else:
turn = 0
end
end
end
Description
Two cowboys A and B take turns to shoot at each other. During each turn, cowboy A can hit cowboy B with probability a while cowboy B can hit cowboy A with probability b. The duel terminates until one cowboy succeeds to hit the other.
Which is the probability that one of the two cowboys wins the duel ?
A similar example was first introduced in:
- A. McIver, C. Morgan, Abstraction, Refinement and Proof for Probabilistic Systems. Monographs in Computer Science, Springer 2005, ISBN 978-0-387-40115-7, (pag. 211), [Link]
| Program features | Value | Dependency Graph |
|---|---|---|
| if statements | Yes | (L) Linear (NL) nonlinear 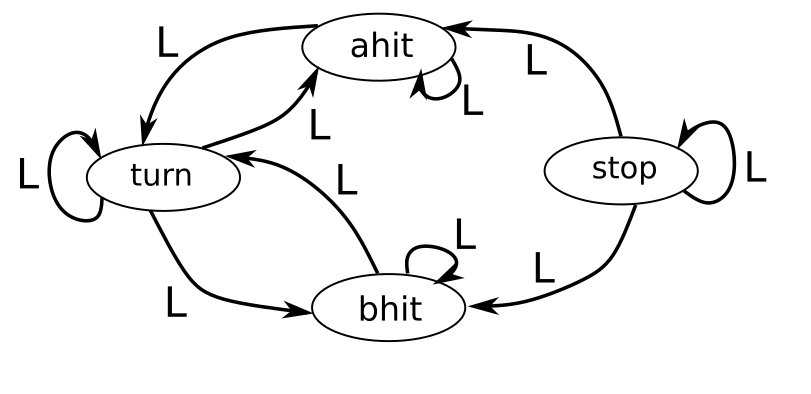 |
| State space | Finite, discrete | |
| Circular Dependency | Yes | |
| Symbolic Constants | Yes (a, b) | |
| Effective Variables | Yes (turn, continue, ahit, bhit) | |
| Defective Variables | No |
Solving the problem using POLAR:
The probability that Cowboy A will finally win can be calculated using POLAR as: \[\mathbb{E} (ahit) = \frac{a (a (a + b - 1)^{(n - 1)} + b - (a + b - 1)^{(n - 1)} - 1)}{(a+b-2)}\]
POLAR transforms the original program by replacing the if-then-else statements as assignments:
types
turn : Finite(0, 1)
stop : Finite(0, 1)
ahit : Finite(0, 1)
bhit : Finite(0, 1)
_old0 : Finite(0, 1)
_stop1 : Finite(0, 1)
_turn1 : Finite(0, 1)
end
turn = 0
stop = 0
ahit = 0
bhit = 0
while true:
_old0 = turn
ahit = Bernoulli(a) | _old0 == 0 : ahit
_stop1 = 1 | (ahit == 1 ∧ _old0 == 0) : stop
_turn1 = 1 | (¬(ahit == 1) ∧ _old0 == 0) : turn
bhit = Bernoulli(b) | ¬(_old0 == 0) : bhit
stop = 1 | (bhit == 1 ∧ ¬(_old0 == 0)) : _stop1
turn = 0 | (¬(bhit == 1) ∧ ¬(_old0 == 0)) : _turn1
end
This is the command line for POLAR to compute the closed-form solution of the expected value for the ahit variable:
python polar.py benchmarks/prinsys/duelling_cowboys.prob --goals "E(ahit)"
8888888b. .d88888b. 888 d8888 8888888b.
888 Y88b d88P" "Y88b 888 d88888 888 Y88b
888 888 888 888 888 d88P888 888 888
888 d88P 888 888 888 d88P 888 888 d88P
8888888P" 888 888 888 d88P 888 8888888P"
888 888 888 888 d88P 888 888 T88b
888 Y88b. .d88P 888 d8888888888 888 T88b
888 "Y88888P" 88888888 d88P 888 888 T88b
By the ProbInG group
-------------------
- Analysis Result -
-------------------
E(ahit) = 0; a*(a*(a + b - 1)**(n - 1) + b - (a + b - 1)**(n - 1) - 1)/(a + b - 2)
Solution is exact
Elapsed time: 1.5186586380004883 s
If a and b are both equal to 1 then the program becomes deterministic and
in that case Cowboy A will always win since is the first to shoot. If either a or
b is less than 1 then the limit for n to infinity of (a + b - 1) < 1 is:
\[\lim_{n \to \infty} (a + b - 1)^{(n - 1)} = 0\]
Consequently we have that: \[ \lim_{n \to \infty} \frac{a (a (a + b - 1)^{(n - 1)} + b - (a + b - 1)^{(n - 1)} - 1)}{(a+b-2)} = \frac{a(b - 1)}{a + b - 2}\]
Comparison with Monte Carlo simulation:
| Parameter | Current Value | Tuning |
|---|---|---|
| Number of program executions: | ||
| Number of loop iterations (n): | ||
| Probability (a): | ||
| Probability (b): |
| Exact E(ahit) | Approx. E(ahit) |
|---|---|
Limitation of POLAR in this example:
While we can compute the exact probability for the Cowboy A to win, we have issues to compute the exact probability for the Cowboy B to win using symbolic constants due to some limitations of the library sympy that POLAR is using.
python polar.py benchmarks/prinsys/duelling_cowboys.prob --goals "E(bhit)"
8888888b. .d88888b. 888 d8888 8888888b.
888 Y88b d88P" "Y88b 888 d88888 888 Y88b
888 888 888 888 888 d88P888 888 888
888 d88P 888 888 888 d88P 888 888 d88P
8888888P" 888 888 888 d88P 888 8888888P"
888 888 888 888 d88P 888 888 T88b
888 Y88b. .d88P 888 d8888888888 888 T88b
888 "Y88888P" 88888888 d88P 888 888 T88b
By the ProbInG group
-------------------
- Analysis Result -
-------------------
sorted roots not supported over ZZ[a,b]
However, if we set a and b to a specific value (for example both to 0.5):
turn = 0
stop = 0
ahit = 0
bhit = 0
while true:
if turn == 0:
ahit = Bernoulli(0.5)
if ahit == 1:
stop = 1
else:
turn = 1
end
else:
bhit = Bernoulli(0.5)
if bhit == 1:
stop = 1
else:
turn = 0
end
end
end
Then, we can compute the solution for Cowboy B as follows:
python polar.py benchmarks/prinsys/duelling_cowboys.prob --goals "E(bhit)"
8888888b. .d88888b. 888 d8888 8888888b.
888 Y88b d88P" "Y88b 888 d88888 888 Y88b
888 888 888 888 888 d88P888 888 888
888 d88P 888 888 888 d88P 888 888 d88P
8888888P" 888 888 888 d88P 888 8888888P"
888 888 888 888 d88P 888 888 T88b
888 Y88b. .d88P 888 d8888888888 888 T88b
888 "Y88888P" 88888888 d88P 888 888 T88b
By the ProbInG group
-------------------
- Analysis Result -
-------------------
E(bhit) = 0; 0; 1/4; 1/4; 1/2 - 2**(-n)
Solution is exact
Elapsed time: 0.47222185134887695 s